设二次函数的一般式为(y = ax^{2}+bx + c)((a
eq0))。
# 平移变换
1. 上下平移:
若将二次函数(y = ax^{2}+bx + c)向上平移(k)((k>0))个单位,纵坐标发生变化,横坐标不变,此时函数变为(y = ax^{2}+bx + c + k)。
证明:对于原二次函数(y = ax^{2}+bx + c)图像上任意一点((x,y)),向上平移(k)个单位后,该点坐标变为((x,y + k)),把(y + k)用原函数(y = ax^{2}+bx + c)代换,就得到(y + k = ax^{2}+bx + c + k),即平移后的函数表达式为(y = ax^{2}+bx + c + k)。
同理,若向下平移(k)((k>0))个单位,则函数变为(y = ax^{2}+bx + c - k),证明过程类似,原图像上点((x,y))向下平移后变为((x,y - k)),可得(y - k = ax^{2}+bx + c),进而得出(y = ax^{2}+bx + c - k)。
2. 左右平移:
若将二次函数(y = ax^{2}+bx + c)向左平移(h)((h>0))个单位,此时横坐标发生变化,纵坐标不变,函数变为(y = a(x + h)^{2}+b(x + h)+c)。
证明:设原二次函数(y = ax^{2}+bx + c)图像上任意一点((x,y)),向左平移(h)个单位后,该点坐标变为((x - h,y)),把(x)用(x - h)代换原函数中的(x),即(y = a(x - h + h)^{2}+b(x - h + h)+c = a(x + h)^{2}+b(x + h)+c)。
同理,若向右平移(h)((h>0))个单位,则函数变为(y = a(x - h)^{2}+b(x - h)+c),原图像上点((x,y))向右平移后变为((x + h,y)),把(x)用(x + h)代换原函数中的(x)可得此表达式。
# 轴对称变换
1. 关于(x)轴对称:
若二次函数(y = ax^{2}+bx + c)关于(x)轴对称,那么对应的函数变为(y = - (ax^{2}+bx + c)),即(y = -ax^{2}-bx - c)。
证明:设点((x,y))在原二次函数(y = ax^{2}+bx + c)的图像上,关于(x)轴对称的点坐标为((x,-y)),因为这个对称点在变换后的函数图像上,所以把((x,-y))代入,可得(-y = ax^{2}+bx + c),两边同时乘以(-1)就得到(y = -ax^{2}-bx - c),即变换后的函数表达式。
2. 关于(y)轴对称:
若二次函数(y = ax^{2}+bx + c)关于(y)轴对称,函数变为(y = a(-x)^{2}+b(-x)+c),即(y = ax^{2}-bx + c)。
证明:设点((x,y))在原函数图像上,关于(y)轴对称的点坐标为((-x,y)),因为这个对称点在变换后的函数图像上,将((-x,y))代入可得(y = a(-x)^{2}+b(-x)+c),也就是变换后的函数表达式。
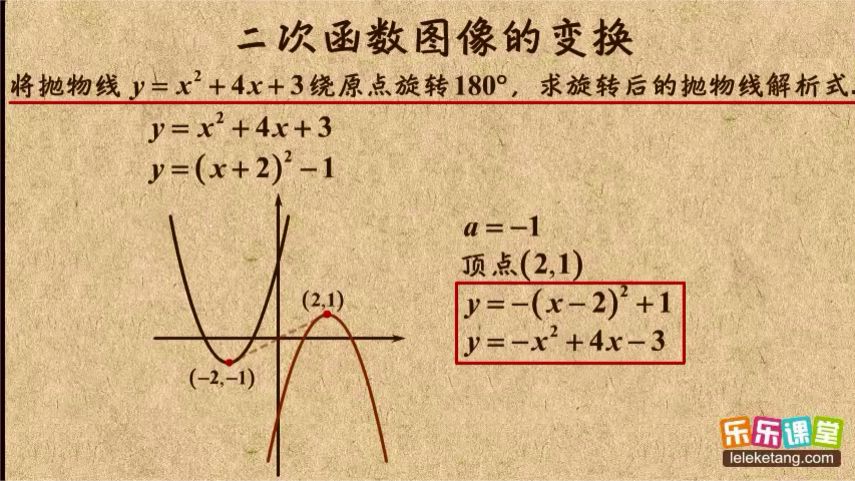
# 中心对称变换
若二次函数(y = ax^{2}+bx + c)关于原点对称,设点((x,y))在原函数图像上,关于原点对称的点坐标为((-x,-y)),把((-x,-y))代入原函数可得(-y = a(-x)^{2}+b(-x)+c),即(-y = ax^{2}-bx + c),两边同时乘以(-1),得到(y = -ax^{2}+bx - c),所以二次函数(y = ax^{2}+bx + c)关于原点对称后的函数表达式为(y = -ax^{2}+bx - c)。













